Calculus I

A core and fundamental course

What is Calculus and used for?

The formal study of calculus started from the 17th century by well-known scientists and mathematicians Isaac Newton and Gottfried Leibniz. Calculus is a mathematical discipline that is primarily concerned with functions, limits, derivatives, integrals and infinite series. The emphasis is understanding concepts. The most fundamental concept in calculus is limit.

The Precise Definition of a Limit

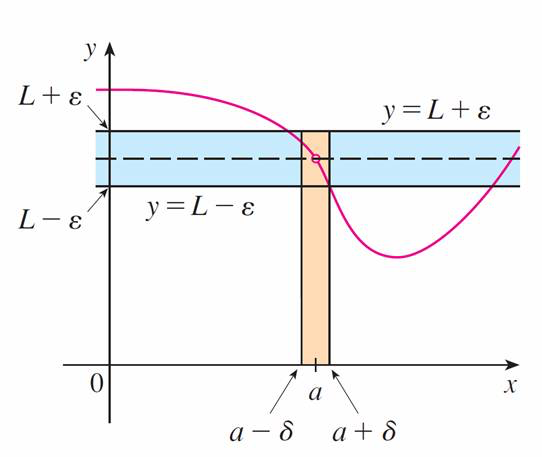Let $ f(x) $ be a function defined on some open interval that contains $ a $, except possibly at $ a $ itself. Then we say that the limit of $ f(x) $ as $ a $ approaches $ a $ is $ L $, and we write $$ \underset{x\rightarrow a}\lim f(x)=L $$ if for every number $ ϵ > 0 $ there is a number $ δ > 0 $ such that $$ \text{if}\quad 0<|x-a|<\delta\quad\text{then}\quad|f(x)-L|<\epsilon $$

Continuity

Let $ f $ be a function and let $ a\in\mathbb{R} $. The function $ f $ is said to be continuous at the point $ a $ if the following three things are true:

1. $ f (a) $ is defined (that is, $ a $ is in the domain of $ f $.)
2. The limit $ \underset{x\rightarrow a}\lim f(x) $ exists.
3. $ \underset{x\rightarrow a}\lim f(x)=f(a) $

Derivative

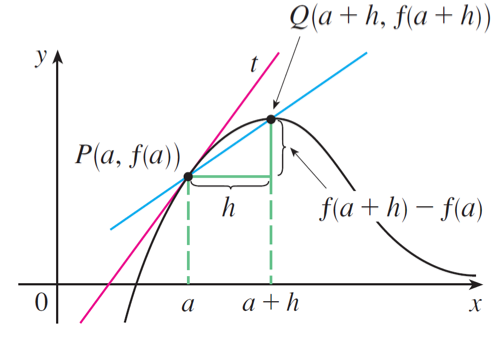
The derivative of a function $ f $ at a number $ a $, denoted by $ f'(a) $, is $$ f'(a)=\underset{h\rightarrow 0}\lim\frac{f(a+h)-f(a)}{h} $$ if this limit exists.

MIT Mathematics

Calculus is the study of how things change. It provides a framework for modeling systems in which there is change, and a way to deduce the predictions of such models.

Calculus is an exciting subject, justly considered to be one of the greatest achievements of the human intellect. I hope you will discover that it is not only useful but also intrinsically beautiful.

— James Stewart

Reference Textbook

Calculus, James Stewart, The 8th, metric edition, Cengage Learning.

Reference Videos by Professor Leonard